Matemáticas 4 COBAO, 408: Tema 2: Funciones polinomiales

II.Funciones polinomiales

En matemáticas, una función polinómica o polinomial es una función asociada a un polinomio con coeficientes en un anillo conmutativo (a menudo un cuerpo).

Formalmente, es una función:

$f:x \mapsto P(x)\,$

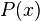donde $P(x)\,$ es un polinomio definido para todo número real $x\,$ ; es decir, una suma finita de potencias de $x\,$ multiplicados por coeficientes reales, de la forma:

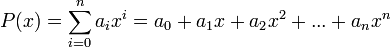
$P(x) = \sum_{i=0}^n a_i x^i = a_0+a_1x+a_2x^2+...+a_nx^n$ Funciones básicas:

Algunas funciones polinómicas reciben un nombre especial según el grado del polinomio:

Grado	Nombre	Expresión
0	función constante	y = a
1	función lineal	y = ax + b es un binomio del primer grado
2	función cuadrática	y = ax² + bx + c es un trinomio del segundo grado
3	función cúbica	y = ax³ + bx² + cx + d es un cuatrinomio de tercer grado

Función lineal.

Una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es unalínea recta. Esta función se puede escribir como:

$f(x) = m x + b \,$

donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica mentonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.

Algunos autores llaman función lineal a aquella con b= 0 de la forma:

$f(x) = m x \;$

mientras que llaman función afín a la que tiene la forma:

$f(x) = m x + b \;$

cuando b es distinto de cero.

Ejemplo.

Una función lineal de una única variable dependiente x es de la forma:

$y = m \; x + b \,$

que se conoce como ecuación de la recta en el plano x,y.

En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

$y = 0,5\; {x} + 2 \,$

en esta recta el parámetro m= 1/2 por tanto de pendiente 1/2, es decir, cuando aumentamos x en una unidad entoncesy aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2.

En la ecuación:

$y = -{x} + 5 \,$

la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de x aumenta en una unidad, el valor de ydisminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.

En una recta el valor de m se corresponde al ángulo $\theta\,$ de inclinación de la recta con el eje de las x a través de la expresión:

$m = \tan \theta \,$

Aqui la gráfica de lo anterior. ------------------------->

Función cuadrática.

una función cuadrática o función de segundo grado es una función polinómica definida como:

$f(x) = ax^2 + bx + c \,$

en donde a, b y c son números reales (constantes) y a es distinto de 0.

La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.

La derivada de una función cuadrática es una función lineal y su integral una función cúbica.

Ejercicios.

Identifica cuál de las siguientes funciones corresponden a una función constante, lineal o cuadrática:

f(x)=20
f(x)=x²
f(x)=1+k²
f(x)=m
f(x)=(x+ 2)(x - 4)
f(t)= k
f(t)=5
f(t)=r²
f(s)=2s
f(x)= e

Función polinomial de grado cuatro (función cuártica).

Una ecuación de cuarto grado o ecuación cuártica con una incógnita es una ecuación que se puede poner bajo la forma canónica:

$ax^4 + bx^3 + {cx^2}^{} + dx + e = 0$

donde a, b, c, d y e (siendo $a \ne 0$ ) son números que pertenecen a un cuerpo, usualmente a los reales $\mathbb{R}$ o los complejos $\mathbb{C}$ .

Ejemplo.

Sea K un cuerpo, donde se pueden extraer raíces cuadradas y cúbicas (y por lo tanto también de cuarto orden, pues equivale a extraer raíces cuadradas dos veces seguidas). En este cuerpo, es posible factorizar por todo a, y la identidad siguiente es válida:

$(a - b)^4 = a^4 - 4a^3b + 6a^2b^2 - 4ab^3 + b^4 \,$ .

Gráfica de una ecuación de cuarto grado.

Ejercicios.

x⁴ - 5x²+4 = 0

x⁴ - 4 = x² – 1

x^4 - 5x² = 36

2x^4 - x - 14x^3 - 5x² = -6

Matemáticas 4 COBAO, 408

martes, 19 de marzo de 2013

Tema 2: Funciones polinomiales

II.Funciones polinomiales

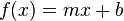
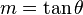
No hay comentarios:

Publicar un comentario