I. Relaciones y funciones.
Entender los conceptos de Relación y de Función es de suma importancia en Matemática.
Para lograr esa comprensión es necesario adentrarnos en la noción de Correspondencia, ya que esta tiene un papel fundamental en las relaciones y funciones.
Lo primero es entender que Correspondencia es equivalente a Relación. En nuestra lengua, decir “en relación a”, es equivalente a decir “corresponde a”.
Ejemplos:
En una tienda comercial, cada artículo está relacionado con su precio; o sea, a cada artículo le corresponde un precio.
En la guía telefónica, cada cliente está relacionado con un número; o sea, a cada nombre de la guía le corresponde un número.
Definición matemática de Relación y de Función
En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamadoRecorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones sonfunciones.
También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.
Plano Cartesiano
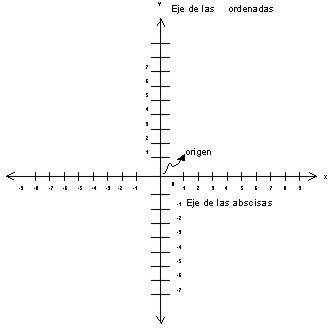
El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.
Las coordenadas se forman asociando un valor del eje de las equis a uno de las yes, respectivamente, esto indica que un punto (P) se puede ubicar en el plano cartesiano tomando como base sus coordenadas, lo cual se representa como:
P (x, y)
Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia la izquierda si son negativas, a partir del punto de origen, en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes (en el eje de las ordenadas) hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas ambas coordenadas.
.........................................................................................................................................................................................................................
Dados dos conjuntos A y B una relación definida de A en B es un conjunto de parejas ordenadas (par ordenado) que hacen verdadera una proposición; dicho de otro modo, una relación es cualquier subconjunto del producto cartesiano A x B
Ejemplo 1.
Si A = {2, 3} y B = {1, 4, 5}, encontrar tres relaciones definidas de A en B.
Solución
El producto cartesiano de A x B está conformado por las siguientes parejas o pares ordenados:
A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y cada uno de los siguientes conjuntos corresponde a relaciones definidas de A en B:
R1 = {(2, 1), (3, 1)}
R2 = {(2, 4), (2, 5), (3, 4), (3, 5)}
R3 = {(2, 4), (3, 5)}
La relación R1 se puede definir como el conjunto de pares cuyo segundo elemento es 1, esto es, R1 = {(x, y) / y = 1}.
La relación R2 está formada por los pares cuyo primer componente es menor que el segundo componente, R2 = {(x, y) / x < y}
Y la relación R3 está conformada por todos los pares que cumplen con que el segundo componente es dos unidades mayor que el primer componente, dicho de otro modo, R3 = {(x, y) / y = x + 2}
Así, se puede continuar enumerando relaciones definidas a partir de A x B. Como se puede ver, la regla que define la relación se puede escribir mediante ecuaciones o desigualdades que relacionan los valores de x e y. Estas reglas son un medio conveniente para ordenar en pares los elementos de los dos conjuntos.
Ejemplo 2.
Dados los conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares ordenados (x, y) que satisfagan la relación
R = {(x, y) / x + y = 3}
Solución
El producto cartesiano de C x D está formado por los siguientes pares ordenados
C x D = {(1, 2), (1, 3), (1, 6), (–3, 2), (–3, 3), (–3, 6)}
Las parejas ordenadas que satisfacen que la suma de sus componentes sea igual a 3 son:
R = {(1, 2), (–3, 6)}
Toda relación queda definida si se conoce el conjunto de partida, el conjunto de llegada y la regla mediante la cual se asocian los elementos. En el ejemplo anterior, el conjunto de partida corresponde al conjunto C, el conjunto de llegada es el conjunto D y la expresión x + y = 3 es la regla que asocia los elementos de los dos conjuntos.
Dominio, contradominio, argumento, imagen y rango de una relación
El dominio de una función es el primer conjunto de datos, sus elementos (argumentos) tienen su imagen en el contradominio.
El argumento es cualquier elemento del dominio.
La imagen es el elemento que le corresponde a un argumento de forma particular.
El contradominio de una función es el segundo conjunto de datos, contiene a las imágenes.
El rango está conformado por el conjunto de imágenes, algunas veces es igual al contradominio.
Ejemplo 3
El argumento es cualquier elemento del dominio.
La imagen es el elemento que le corresponde a un argumento de forma particular.
El contradominio de una función es el segundo conjunto de datos, contiene a las imágenes.
El rango está conformado por el conjunto de imágenes, algunas veces es igual al contradominio.
Ejemplo 3
Sea A = {1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R la relación definida de A en B determinada por la regla “y es el doble de x” o “y = 2x”, encontrar dominio y rango de la relación.
Solución
El total de pares ordenados que podemos formar, o producto cartesiano es:
A x B = {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R (y = 2x) son solo:
R = {(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: “4 es el doble de 2”; esto es, “4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”.
Así, el dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de partida?
En el Dominio falta el elemento 1 del conjunto de partida, por lo tanto el Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de llegada es elemento del rango?
La respuesta es no, pues en el rango faltan el 5 y el 7.
Representación gráfica de las relaciones
Los pares ordenados se pueden representar gráficamente por medio de diagramas sagitales o por medio de puntos en el plano cartesiano. Veamos el siguiente ejemplo.
Ejemplo 4
Si A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y R la relación definida por la regla
R = {(x, y) / y = 2x + 1}, graficar R.
Solución
Los pares ordenados que pertenecen a la relación (que cumplen con y = 2x + 1) son:
R = {(1, 3), (2, 5), (3, 7), (4, 9)}
La gráfica que corresponde es:
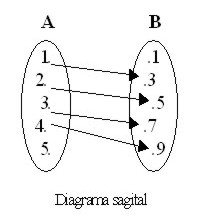 | 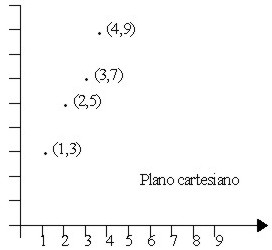 |
Ejercicios:
- f(2)
- f(-1)
- f(3a)
- f(b-3)
- Si g(t)=(t-1)^1/2, halle si es posible g(3), g(5), g(1) y g(-1)
FUNCIONES CONTINUAS Y DISCONTINUAS
Muchas funciones tienen la propiedad de que no hay "cortes" en sus gráficas. Por ejemplo, compare las funciones:
Cuyas gráficas aparecen en las figuras 9.23 y 9.24, respectivamente. Cuando x = 1, la gráfica de f no se corta, pero la de g sí tiene un corte.
Poniéndolo de otra manera, si tuviera que trazar ambas gráficas con un lápiz, tendría que levantar el lápiz de la gráfica de g, cuando x = 1, pero no lo tendría que levantar de la gráfica de f. Estas situaciones pueden expresarse por medio de límites.
Cuando x se aproxima a 1, compare el límite de cada función con el valor de la función en x = 1.
Mientras que
El límite de f cuando x —> 1 es igual a f (1), pero el límite de g cuando x —> 1 no es igual a g (1). Por estas razones decimos que f es continua en 1 y g discontinua en 1.
Funciones inyetiva, sobreyectiva y biyectiva
| Funciones | Inyectiva | No inyectiva | ||
| Sobreyectiva |
|  | ||
| No sobreyectiva |  |  |
- Se dice que una función f : A → B es inyectiva si las imágenes de elementos distintos son distintas:
- o, de modo equivalente, si sólo asigna imágenes idénticas a elementos idénticos:
- Una función f : A → B se dice suprayectiva (o sobreyectiva) si su imagen es igual a su codominio:
- o, de modo equivalente, si todo elemento del codominio es la imagen de algún elemento del dominio:
Las funciones inyectivas no repiten las imágenes: si b = f(a), ningún otro a' tiene por imagen a b, por lo que la anti-imagen de este último sólo contiene al elemento a. Las funciones suprayectivas recorren todo el codominio, por lo que ninguna anti-imagen puede estar vacía. La definición de función suprayectiva asume que esta tiene un codominio especificado previamente. De lo contrario, la noción de suprayectividad no tiene sentido.
Cuando una función tiene ambas propiedades a la vez, se dice que es una biyección entre ambos conjuntos:
|
Las funciones biyectivas constituyen un «emparejamiento perfecto» entre los elementos del dominio y el codominio: cada elemento en A tiene una única «pareja» en B—como todas las funciones—, y a cada elemento de B le corresponde uno solo en A —al menos uno por ser suprayectiva, y como mucho uno por ser inyectiva—.
- Ejemplos.
- La función cubo f: R → R es biyectiva. Es inyectiva porque dos números reales que tienen el mismo cubo son idénticos, y es suprayectiva porque Im(f) = R.
- La función «inverso» g: R \ {0} → R es inyectiva, ya que el inverso de cada número real no nulo es único (1/x = 1/y implica necesariamente que x = y). Sin embargo no es suprayectiva, dado que Im(g) = R \ {0}.
- La función de clasificación de mamíferos γ: M → G no es inyectiva, ya que hay mamíferos distintos en el mismo género (por ejemplo, γ(Yak) = γ(Toro) = Bos). Sin embargo sí es suprayectiva, ya que en cada género de mamíferos hay clasificada al menos una especie de mamíferos.
- La función área A: T → R no es sobreyectiva, ya que Im(A) = R+. Tampoco es inyectiva, ya que pueden construirse con facilidad triángulos distintos con el mismo área.
Función identidad
En cualquier conjunto puede definirse una función identidad, que teniendo como dominio y codominio al propio conjunto, asocia cada elemento consigo mismo.
|
También se denota como IA. La función identidad actúa como un elemento neutro al componer funciones, ya que no «hace nada».
|
Es decir, dado un elemento x ∈ A, se tiene que:
Función inversa
Una función puede tener inversa, es decir, otra función que al componerla con ella resulte en la identidad, del mismo modo que un número multiplicado por su inverso da 1.
|
No todas las funciones son invertibles, sino que solo aquellas que sean biyectivas poseen inversa:
|
La notación para funciones inversas puede ser confusa. Para un elemento del codominio b, f−1(b) puede denotar tanto la anti-imagen de b (un subconjunto del dominio), como a la imagen de b por la función inversa de f (un elemento del dominio), en el caso de que f sea invertible.
- Ejemplos.
- La función «exponencial» h: R → R, que asocia a cada número real su exponencial, h(x) = ex, no es invertible, ya que no es suprayectiva: ningún número negativo pertenece a la imagen de h.
- Existe una función que calcula el cambio entre dos divisas. En el caso del cambio de rupias a quetzales (las monedas de la India y Guatemala), la conversión está dada (en 2011) por:
Q(r) = 0,15 × r
Esta función de cambio tiene inversa, la conversión recíproca de quetzales a rupias:
R(q) = 6,65 × q - La función cubo f(x) = x3 es invertible, ya que podemos definir la función inversa mediante la raíz cúbica, f−1(x) = 3√x.


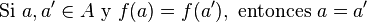


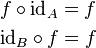


No hay comentarios:
Publicar un comentario