domingo, 26 de mayo de 2013

Tema 6: Funciones periódicas


Funciones periódicas


En matemática, una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período, o sea:
f \left ( x \right ) = f \left ( x + P \right )
donde P es el período.
De la misma manera, pero en un contexto físico, las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:
x_a (t) = x_a (t+T_p) = x_a (t+nT_p) \,\!
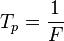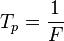donde el periodo propio fundamental T_p = \frac {1}{F} \,\!, F \,\! es la frecuencia de la componente fundamental de la onda periódica y n \,\! un número entero.

Estas pueden ser Funciones trigonométricas y Funciones circulares, las cuales son:

Función seno:

En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la hipotenusa:
\sin\ \alpha=\frac{a}{c}
O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c=1):
\sin\ \alpha=a \,
En matemáticas el seno es la función obtenida al hacer variar la razón mencionada, siendo una de las funciones trascendentes.


Función coseno:


En trigonometría el coseno (abreviado cos) de un ángulo agudo en un triángulo rectángulo se define como la razón entre el cateto adyacente a ese ángulo y la hipotenusa:
\cos\alpha = \frac{b}{c}
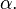
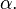
En virtud del Teorema de Tales, este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una función del ángulo  \alpha.
Otro modo de obtener el coseno de un ángulo consiste en representar éste sobre la circunferencia goniométrica, es decir, la circunferencia unitaria centrada en el origen. En este caso el valor del coseno coincide con la abscisa del punto de intersección del ángulo con la circunferencia. Esta construcción es la que permite obtener el valor del coseno para ángulos no agudos.
En análisis matemático el coseno es la función que asocia un número real  x  con el valor del coseno del ángulo de amplitud, expresada en radianes,  x . Es una función trascendente y analítica, cuya expresión en serie de potencias es
\begin{array}{rl} \cos x = & 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots \\ \\ = & \sum_{n=0}^\infty \; (-1)^n \; \frac{x^{2n}}{(2n)!} \end{array}
La serie de potencias anterior proporciona a su vez la extensión de la función coseno al plano complejo del siguiente modo:
{\rm cos\ }z=\frac{e^{iz} + e^{-iz} }{2}
Donde i es la unidad imaginaria.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)