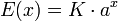Matemáticas 4 COBAO, 408: mayo 2013

martes, 28 de mayo de 2013

Tutorial: División sintética

https://www.youtube.com/watch?v=yUUhtRpVCfg

En el link de arriba podrán encontrar un tutorial para que chequen el procedimiento de la división sintética, si no entra directo, solo copien y peguen en la barra de dirección de su navegador.

domingo, 26 de mayo de 2013

Tema 6: Funciones periódicas

Funciones periódicas

En matemática, una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período, o sea:

$f \left ( x \right ) = f \left ( x + P \right )$

donde P es el período.

De la misma manera, pero en un contexto físico, las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:

$x_a (t) = x_a (t+T_p) = x_a (t+nT_p) \,\!$

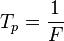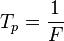donde el periodo propio fundamental $T_p = \frac {1}{F} \,\!$ , $F \,\!$ es la frecuencia de la componente fundamental de la onda periódica y $n \,\!$ un número entero.

Estas pueden ser Funciones trigonométricas y Funciones circulares, las cuales son:

Función seno:

En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la hipotenusa:

$\sin\ \alpha=\frac{a}{c}$

O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c=1):

$\sin\ \alpha=a \,$

En matemáticas el seno es la función obtenida al hacer variar la razón mencionada, siendo una de las funciones trascendentes.

Función coseno:

En trigonometría el coseno (abreviado cos) de un ángulo agudo en un triángulo rectángulo se define como la razón entre el cateto adyacente a ese ángulo y la hipotenusa:

$\cos\alpha = \frac{b}{c}$

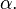
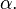
En virtud del Teorema de Tales, este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una función del ángulo $\alpha.$

Otro modo de obtener el coseno de un ángulo consiste en representar éste sobre la circunferencia goniométrica, es decir, la circunferencia unitaria centrada en el origen. En este caso el valor del coseno coincide con la abscisa del punto de intersección del ángulo con la circunferencia. Esta construcción es la que permite obtener el valor del coseno para ángulos no agudos.

En análisis matemático el coseno es la función que asocia un número real $x$ con el valor del coseno del ángulo de amplitud, expresada en radianes, $x$ . Es una función trascendente y analítica, cuya expresión en serie de potencias es

$\begin{array}{rl} \cos x = & 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots \\ \\ = & \sum_{n=0}^\infty \; (-1)^n \; \frac{x^{2n}}{(2n)!} \end{array}$

La serie de potencias anterior proporciona a su vez la extensión de la función coseno al plano complejo del siguiente modo:

${\rm cos\ }z=\frac{e^{iz} + e^{-iz} }{2}$

Donde i es la unidad imaginaria.

domingo, 12 de mayo de 2013

Tema: 5 Función exponencial y logaritmica

Función exponencial

La función exponencial, es conocida formalmente como la función real e^x, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=e^x o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.

En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma

$E(x)=K \cdot a^x$

siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.

Ejemplos: Simplifica.

Ejemplo: Halla el valor de x en e ^{x + 1} = e ^{3x - 1}

Práctica:

1) Simplifica: (e ^{3x + 1}) (e ^{2x – 5})

2) Halla el valor de x en e^{3x – 4} = e^2x

Función logarítmica

Una función logarítmica es aquella que genéricamente se expresa como f (x) == log_ax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.

La función logarítmica es la inversa de la función exponencial (ver t35), dado que:

log_a x = b Û a^b = x.

Representación gráfica de funciones logarítmicas y de sus inversas (exponenciales).

Propiedades de la función logarítmica

Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la función exponencial. Así, se tiene que:

La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (0,+¥).
Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales, luego el recorrido de esta función es R.
En el punto x = 1, la función logarítmica se anula, ya que log_a 1 = 0, en cualquier base.
La función logarítmica de la base es siempre igual a 1.
Finalmente, la función logarítmica es continua, y es creciente para a > 1 y decreciente para a < 1.

Ecuaciones logarítmicas

Cuando en una ecuación la variable o incógnita aparece como argumento o como base de un logaritmo, se llama logarítmica.

La resolución de ecuaciones logarítmicas se basa en los mismos procedimientos utilizados en la resolución de las ecuaciones habituales. Aunque no existen métodos fijos, habitualmente se procura convertir la ecuación logarítmica en otra equivalente donde no aparezca ningún logaritmo. Para ello, se ha de intentar llegar a una situación semejante a la siguiente:

log_a f (x) = log_a g (x)

Entonces, se emplean los antilogaritmos para simplificar la ecuación hasta f (x) = g (x), que se resuelve por los métodos habituales.

También puede operarse en la ecuación logarítmica para obtener una ecuación equivalente del tipo:

log_a f (x) = m

de donde se obtiene que f (x) = a^m, que sí se puede resolver de la forma habitual.

Sistemas de ecuaciones logarítmicas

Cuando en un sistema aparecen una o varias ecuaciones logarítmicas, se denomina sistema de ecuaciones logarítmicas. En el caso de un sistema de dos ecuaciones con dos incógnitas, se pueden producir tres casos distintos:

Un sistema formado por una ecuación polinómica y una logarítmica.
Un sistema constituido por dos ecuaciones logarítmicas.
Un sistema compuesto por una ecuación polinómica y una ecuación exponencial.

En cada caso, se utilizan los métodos habituales de resolución de sistemas de ecuaciones, teniendo siempre presente que estas ecuaciones han de transformarse en otras equivalentes, donde la incógnita no aparezca en el argumento o la base del logaritmo, ni en el exponente de la función exponencial.

Ejemplo 1

Despejar las incognitas:

$a) log_{2} 8 = y$
$b) log_{4} x = - \frac {1}{2}$
$c) log_{b} 25 = 2$

Ejemplo 2

Aplicar las leyes de los logaritmos para evaluar:

$log_{2}80 - log{2}5$