Raíces de una Función Racional
Definición:
Una raíz a de una función racional f es el valor donde f(a)=0 |
Lo anterior significa que, para encontrar las raíces de la función polinómica f, tenemos que resolver la ecuación f(x)=0. Para que la función exista, el denominador debe ser distinto de cero. Por lo tanto para encontrar las raíces de la función polinómica , si P(x) y Q(x) no tienen factor comun, es suficiente resolver P(x)=0.
La raíz de una función racional es el valor donde el numerador, P(x)=0 |
Ejemplos:
1.- Encontrar las raíces de la función
Por lo tanto:
Las raíces de la función son x=0, x=1 y x=-2
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
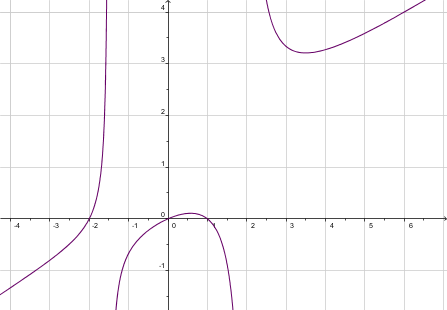
2.-Encontrar las raíces de la función
Solución:Factorizando el numerador en la expresión obtenemos:
Como el denominador no puede ser igual a cero. La función puede ser cero si alguno de los factores del numerador es cero:
Las raíces de la función son x=0, x=-1 y x=-4
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:







Solución:
Recordemos que el denominador no puede ser igual a cero. Por lo tanto, para encontrar las raíces de la función racional solo es necesario encontrar las raíces del numerador. Factorizando el numerador obtenemos:
o
|
o
|
Las raíces de la función son x=0, x=1 y x=-2
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

Como el denominador no puede ser igual a cero. La función puede ser cero si alguno de los factores del numerador es cero:
o
|
o
|
Las raíces de la función son x=0, x=-1 y x=-4
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

----------------------------------------------------------------------------------------------------------------------------------
Asíntotas de una gráfica de una función racional
Las asíntotas son rectas a las cuales la función se va aproximando indefinidamente, cuando por lo menos una de las variables (x o y) tienden al infinito.
Una definición más formal es:
Si un punto (x,y) se desplaza continuamente por una función y=f(x) de tal forma que, por lo menos, una de sus coordenadas tienda al infinito, mientras que la distancia entre ese punto y una recta determinada tiende a cero, esta recta recibe el nombre de asíntota de la función.
Las asíntotas se clasifican en:
-Verticales
-Horizontal
-Oblicuas
Asíntotas horizontales y oblicuas en una función racional
Horizontales:

Ejemplos de asíntotas horizontales

Oblicuas:

Ejemplos de asíntotas oblicuas



No hay comentarios:
Publicar un comentario